20151123-20151129:
Deeper analyzes about isometric projection, which angles and height I wanted to work with before creating images. The “true” isometric projection with 120° between each axis had the “look” that I wanted (instead of the “military perspective”), but as in a lot of other games I went for the 2:1 dimetric projection instead because of the relations between width and height.
20151130-20151213: Implementing the near-isometric projection view.
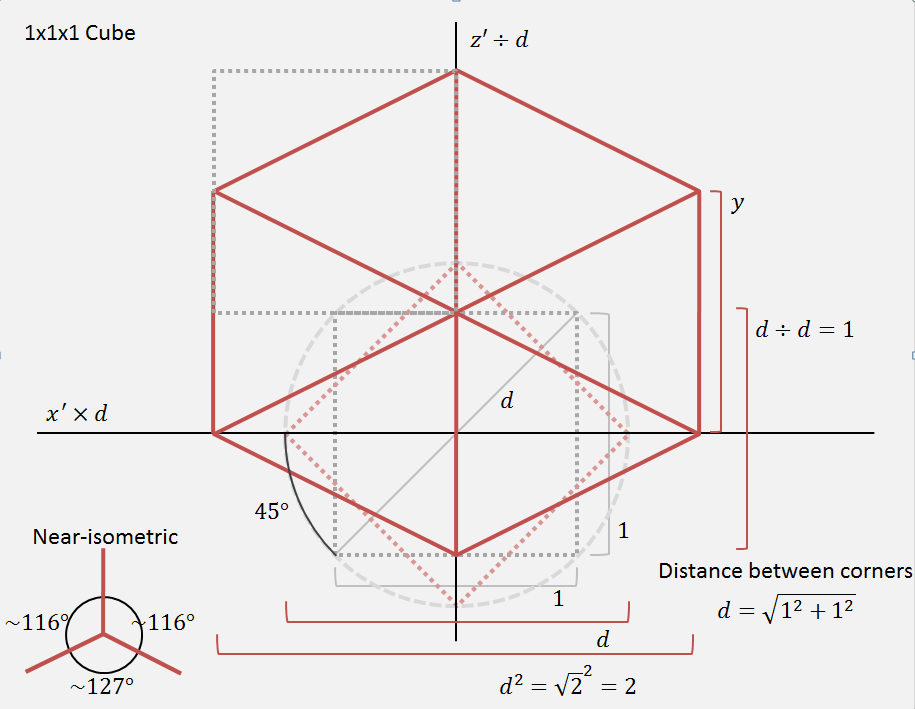
The conversion to canvas coordinates will now be altered as I´ve illustrated in this picture.
The dotted square represents a 1x1x1 Cube seen from above. When rotating it 45° around a surrounding circle (red dotted square), the width and depth of the cube on screen will grow to the distance between its corners (using Pythagorean theorem) or diameter of the surrounding circle (1*d). By dividing the rotated Z points with this distance, the depth will shrink to 1 again (1*d/d). And by multiplying the rotated X points with this distance, the width will grow to 2 (1*d*d) since the distance is the square root of 2. In this way, I don´t need to do further calculations with Y and the rotated view will have a 2:1 relation as the lined red cube.
I´ve tested my formula on rotations in world-space and then in object-space and it works for me. Now I can create images to represent a displayed 1x1x1 area like the cube in my illustration and be able to use it anywhere in the world.
Earlier I tried to divide the rotated Z with 2 and Y with the distance to have this 2:1 relation, but this led to more calculations everywhere in the code. So when I redesigned the rotation with this, things got easier to read and work with.